「CS231n Course 3」神经网络简介
Part 0 前言
参考资料:
- b站 CS231n 4.1 反向传播
- b站 CS231n 4.2 神经网络
- 知乎 反向传播笔记
- 神经网络笔记1(上)
- CS231n Backprop Note(official)
- 神经网络笔记1(下)
- CS231n Neural Network Note-1(official)
Part 1 反向传播
反向传播,Back Propagation(BP),是利用链式法则(chain rule)递归计算表达式的梯度的方法。
核心问题
对给定函数$f(x)$,其中$x$是输入数据的向量,需要计算函数$f$关于$x$的梯度$\nabla f(x)$。
目的
在神经网络中,$f$ 对应的是损失函数 $L$,输入 $x$ 中包含训练数据和神经网络的权重。
例子:对于 SVM,损失函数是 SVM 的损失函数,输入包含了训练数据 $(x_i, y_i), i=1 … N$,权重 $W$,偏差 $b$。训练集是给定的,权重是可以控制(更新)的变量。因此,在实践上,尽管可以计算输入数据 $x_i$ 上的梯度,但是为了进行参数更新,通常只计算参数(如 $W, b$ )的梯度。而 $x_i$ 的梯度在一些情形如可视化以直观理解时可以用上。
从(标量)简单表达式引入
考虑一个简单的二元乘法函数:
对$x$和$y$分别求偏导数:
(偏)导数的意义是,当函数变量在某个点周围的极小区域内变化,而导数是变量变化导致的函数在该方向上的变化率,数学定义如下:
梯度
梯度$\nabla f$是偏导数的向量,因此(继续上面的例子)有:
特别地,即使梯度实际上是一个向量,但通常仍会使用类似”$x$上的梯度“的(非正式)表述,而非”$x$的偏导数“的正确说法,这是因为前者更简单。
对加法求偏导
对$max$求导
该式说明如果该变量比另一个大,则梯度是 $1$,反之为 $0$。
使用链式法则计算复合表达式
对于复杂的包含多个函数的复合函数,如:
可以将其拆分为两个部分:
对其分别求偏导:
值得注意的是,$q$ 是我们构造的中间量,我们实际上不关心 $q$(即,不关心 $\frac{\partial f}{\partial q}$),而关心 $f$ 关于 $x,y,z$ 的梯度。链式法则(chain rule)给出了对于求解 $f$ 关于 $x,y,z$ 梯度表达式的方式:通过相乘。如:
计算图例子
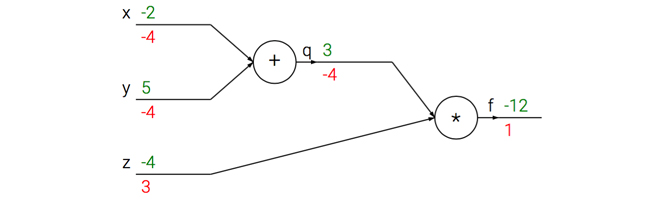
前向传播(forward pass):绿色数字是量的值( $x,y,z$ 的初始值是我们设定的,没有特殊含义),从左到右(前向)进行依次通过算子(节点(node)/门(gate))
反向传播(backword pass):红色数字是 $f$ 相对于当前变量(假定为 $u$ )的梯度,从右到左(反向/后向)依次通过算子进行链式法则。$f$ 的梯度初始值是 $1$,这是因为 $\frac{\partial f}{\partial f} = 1$
直观理解
每个节点(node),也叫做门(gate),具有前向传播和反向传播两种计算:
- 前向传播计算:输入是若干节点的值,输出是经过该节点的运算结果。如上图中$+$门的两个输入是 $-2$ 和 $5$,输出是 $-2+5=3$
- 反向传播计算:输入是链式法则上一步的梯度,输出是链式法则的下一步梯度。如上图中$\times$门的输入是 $1$,输出有两个分支方向,对于 $q$ 方向,由于 $\times$ 运算的偏导数是对方(如$f(x, y) = xy \quad \frac{\partial f}{\partial x} = y \quad
\frac{\partial f}{\partial y} = x$),因此局部梯度为 $z$ 即为 $-4$,因此链式法则的下一步梯度得到 $1 \times (-4) = -4$;对于 $z$ 方向,由于 $\times$ 运算的偏导数是对方,因此局部梯度为 $q$ 即为$3$,因此链式法则的下一步梯度得到 $1 \times 3 = 3$
反向传播可以看作门单元之间在通过梯度信号相互通信。
模块化:以 $Sigmoid$ 为例
上面的例子比较直观,我们给出对门更精确的描述:任何可微函数都可以看作门,可以将多个门组合成一个门,也可以根据需求将一个门拆分为多个门。一个复杂的例子:
事实上,这个表达式描述了一个含输入$x$和权重$w$的2维神经元,使用了 $Sigmoid$ 激活函数。
除了上文的加法门、乘法门和 $max$ 门,还有下述门:
计算图
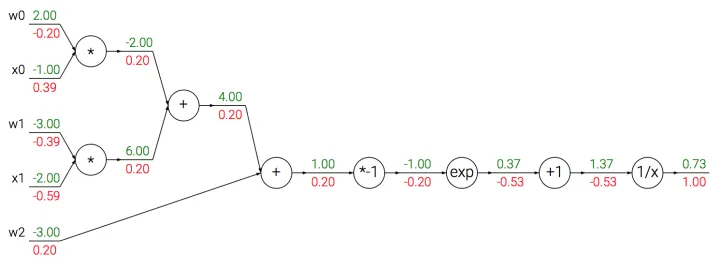
$Sigmoid$
$Sigmoid$ 函数也被记为 $\sigma (x)$,形式如下:
求导结果为:
因此,可以将原式转为:
因此,将原来计算图中的 $*-1,exp,+1,\frac{1}{x}$ 合并为 $\sigma $,一次性算出 $(1-0.73) \times 0.73=0.20$ ,这也说明我们可以根据需求将多个门合并为一个门,也可以将一个门拆分为多个门。
回传流中的模式
多数时候,反向传播中的梯度可以被直观地解释。
加法门
将输出的梯度相等地分发给所有输入,与输入值在前向传播时的值无关。
$max$ 门
$max$ 门将梯度转给其中一个输入,该输入是前向传播中值最大的那个输入。
乘法门
乘法门的局部梯度就是相互交换的输入值,然后根据链式法则乘以输出值的梯度。
对向量操作计算梯度
之前引入的内容都考虑的单个变量,但所有概念都适用于矩阵和向量操作。值得注意的是,操作时需要注意维度和转置操作。
矩阵相乘的梯度
一个有用的技巧:矩阵(向量)的尺寸(维度)和其梯度是一致的,据此我们可以知道如何使维度相符合。比如,$X$的尺寸是$[10, 3]$, $dD$的尺寸是 $[5, 3]$,如果想要 $dW$ 和 $W$ 的尺寸是 $[5, 10]$ ,那么需要 $dD.dot(X.T)$
Part 2 神经网络
线性分类与神经网络
在之前的线性分类笔记中,我们使用了 $s=Wx$ 来计算不同视觉类别的评分,其中 $W$ 是一个权重矩阵, $x$ 是一个包含了图像的全部像素数据的输入列向量。具体地,在CIFAR-10中, $x$ 是 $[3072 \times 1]$ 的列向量,$W$ 是 $[10 \times 3072]$ 的矩阵,输出的评分是 $[10 \times 1]$ 列向量,表示 $10$ 个分类的评分。
而神经网络有所不同,(一个两层神经网络,2-layer Neural Net)的计算公式是:
其中, $W_1$ 的含义是:如,它可以是一个 $[100\times 3072]$ 的矩阵,可以将图像转为一个 $[100 \times 1]$ 的过渡向量。
函数 $max(0, -)$ 是非线性的,会作用于每个元素,称为激活函数,它的选择有很多种。在这里, $max$ 函数简单地设置了阈值,将所有小于 $0$ 的值变为 $0$ 。
矩阵 $W_2$ 的尺寸是 $[10 \times 100]$ ,最终可以得到一个 $[10 \times 1]$ 的列向量,每个元素(数字)可以解释为分类的评分。
在上面,我们注意到神经网络和线性分类的重要区别在于非线性函数。假如没有非线性函数,那么两个矩阵会乘在一起,合并为一个矩阵,那么就会重新变成线性函数(分类)。因此,这个非线性函数就是变化的关键。
参数 $W_1$ 和 $W_2$ 会通过随机梯度下降来学习,他们的梯度在反向传播中通过链式法则求导计算。
类似地,三层神经网络可以看做:
其中, $W_1, W_2, W_3$ 是需要进行学习的参数,中间隐层(hidden layer)的尺寸是网络的超参数,后续会学习如何设置。
神经元(Neuron)
神经网络算法最开始是受到生物神经系统建模的启发,但是很快与其分道扬镳,成为一个工程问题。因此,这方面的讨论局限于高度抽象的简略描述,不做过多的类比牵连。
连接与信号
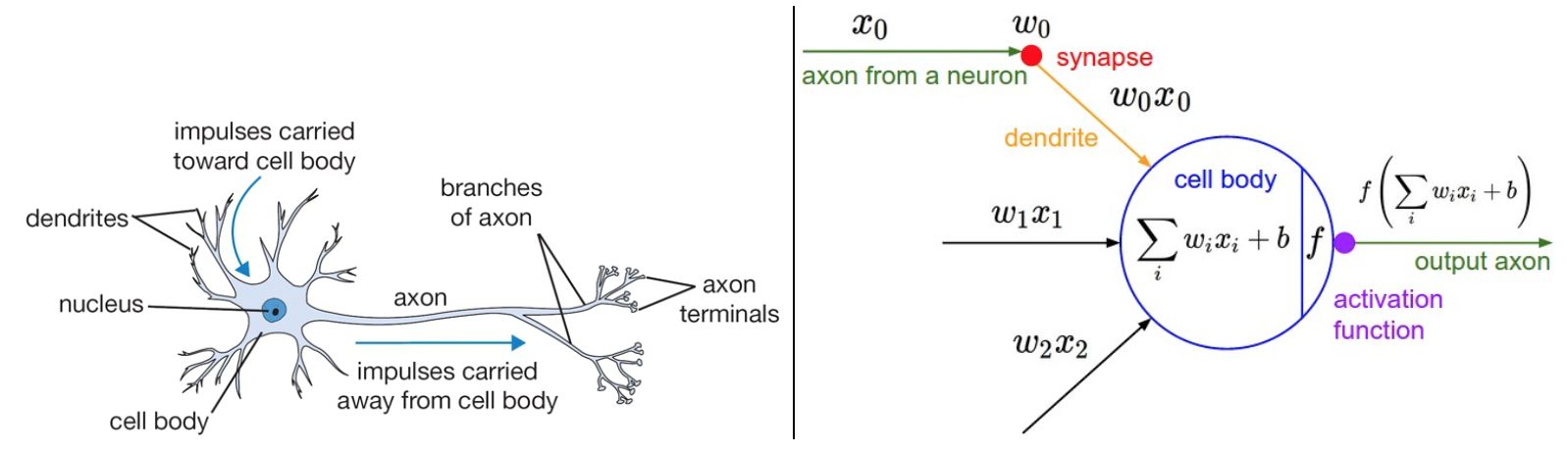
左边是生物神经元,右边是(神经网络中的)神经元计算模型。
- 生物模型中,每个神经元从树突获得输入信号,沿着唯一轴突产生输出信号。轴突在末端会分支,通过突触和其他神经元的树突相连。
- 计算模型中,沿着轴突传播的信号(这里是 $x_0$),传播至下一个神经元时,会基于突触的强度(这里是 $w_0$),和该神经元的树突进行乘法交互(这里是 $w_0x_0$)。这里,突触的强度(也就是权重 $w$ )是可以学习的,而且可以控制一个神经元对另一个神经元影响的强度(还可以控制影响方向:使其兴奋(正权重)或抑制(负权重))
- 生物模型中,树突将信号传递到细胞体,信号在细胞体中相累加,如果和高于某个阈值,则神经元被激活,向其轴突输出一个峰值信号。
- 计算模型中,假设峰值信号的准确时间点不重要,重要的是激活信号的频率。这个基于速率编码(firing rate)的观点将神经元的激活率建模为激活函数(activation function)$f$ ,表达轴突上的激活信号的频率。
- 历史上激活函数常选择使用 sigmoid 函数 $\sigma$,该函数输入实数值(求和后的信号值),将输入值压缩到 0-1 之间。
常用激活函数
$Sigmoid$
$Sigmoid$ 公式如下:
函数图像如下:
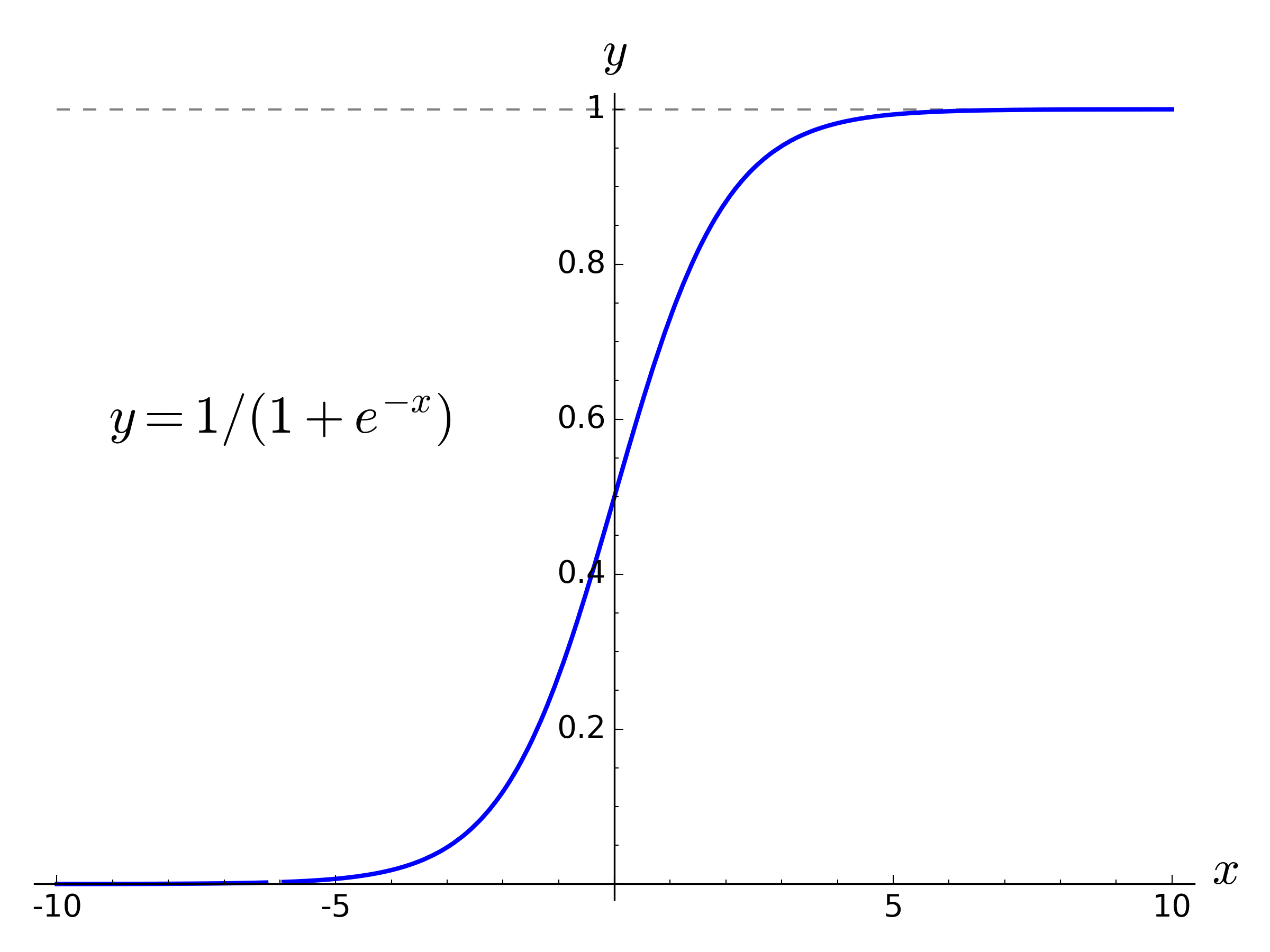
$Sigmoid$ 函数输入实数值,并将其压缩到 $0$ 到 $1$ 的范围内。具体地,很大的负数变为 $0$ ,很大的正数变为 $1$ 。
$Sigmoid$ 对于神经元的激活频率有良好的解释:从完全不激活($0$)到在求和后的最大频率处的完全饱和的激活($1$)。尽管历史上比较常用,但是现在已经很少使用了,因为有两个主要缺点:
- $Sigmoid$ 函数饱和使梯度消失。当神经元的激活在接近 $0$ 或 $1$ 处时会饱和,梯度接近 $0$。由于反向传播时,局部梯度会和输出的梯度相乘,如果局部梯度很小(接近 $0$ ),那么相乘的结果会接近 $0$ ,这回“杀死”梯度。
- $Sigmoid$ 函数的输出不是零中心的。
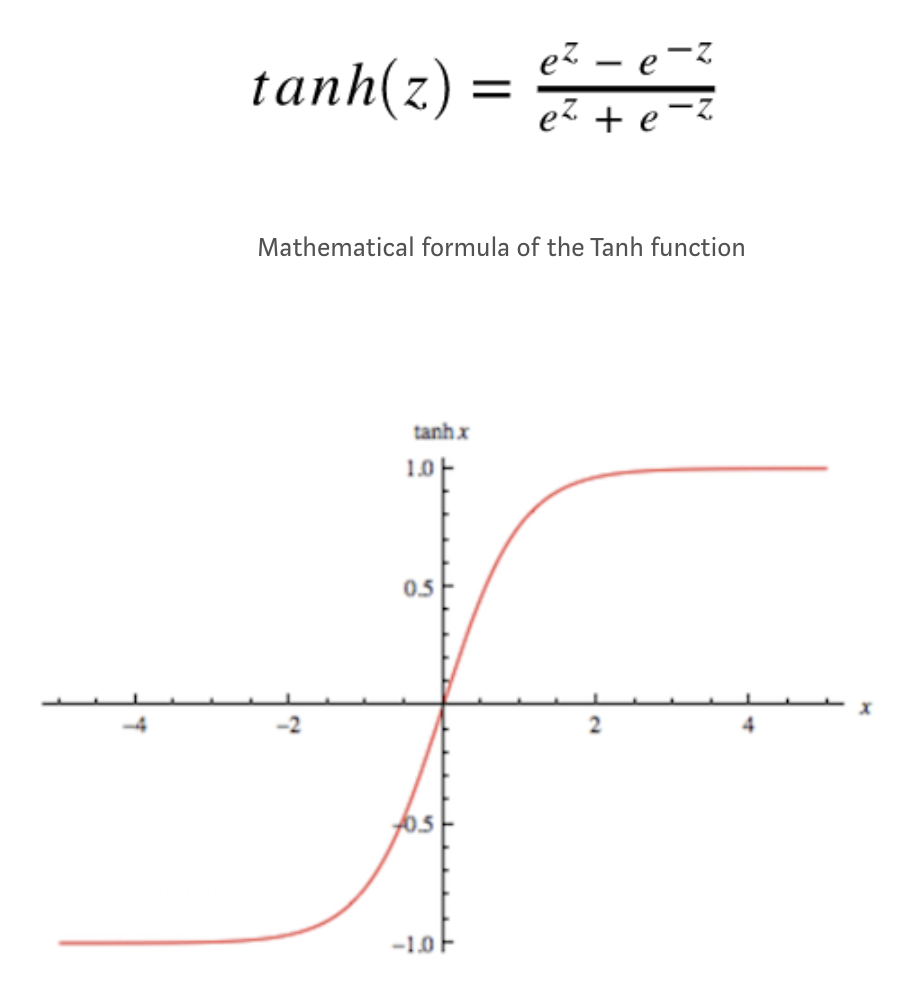
$tanh$
$tanh$ 公式如下:
函数图像如下:
ReLU
ReLU公式如下:
TODO
Leaky ReLU
Leakly ReLU公式如下:
TODO
Maxout
Maxout公式如下:
是 ReLU 和 Leakly ReLU 的一般化归纳。
TODO
神经网络结构
学习神经网络结构非常重要,可以帮助阅读文献的架构图(笔者注)
分层组织(layer-wise organization)
将神经网络算法以神经元的形式图形化。神经网络被建模成神经元的集合,神经元之间以无环图的形式进行连接。这也就是说,一些神经元的输出是另一些神经元的输入。神经网络中不允许循环,因为循环会导致前向传播(正向传播,forward pass)的无限循环。
通常,神经网络模型中的神经元是分层的,这不像生物神经元会聚合成大小不一的团状。对于普通的神经网络,最普通的层的类型是全连接层(fully-connected layer)。
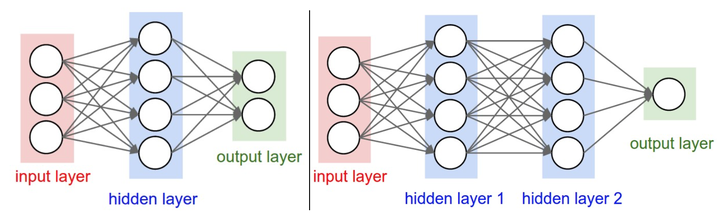
左边是2层神经网络(2-layer neural network),右侧是3层神经网络(3-layer neural network)
全连接层中的神经元与前后两层的神经元是完全成对连接的,但同一个全连接层内的神经元之间没有连接。
上图中左侧的2层神经网络的隐层(hidden layer)包含4个神经元(neural,也可以称为单元unit),输入层由3个神经元组成,输出层由2个神经元组成;右侧图是一个3层神经网络,有2个包含4个神经元的隐层。在这两个神经网络中,层与层之间的神经元是全连接的,但是层内的神经元不连接。
命名规则
当说“N层神经网络(N-layer neural network)”时,并没有将输入层算入。因此,单层的神经网络是没有隐层的(指输入直接映射到输出)。因此,有人认为逻辑回归(logistic regression)和支持向量机(SVM)是一种单层神经网络(single-layer neural network)的特例。
人们也会使用人工神经网络(Artificial Neural Network, ANN)或多层感知器(Multi-Layer Perceptrons, MLP)来指代神经网络(Neural Network, NN)。
也有人不喜欢神经网络算法和人类大脑的类比,他们更倾向于使用单元(unit)而非神经元(neuron)作为术语。
输出层(Output layer)
和神经网络中的其他层不同,输出层的神经元一般没有激活函数(或者认为有一个线性相等的激活函数)。这是因为最后的输出层大多用来表示分类评分值,因此是任意值的实数,或者某种实数值的目标数(比如在回归regession中)。
确定网络尺寸(Sizing neural networks)
用来度量神经网络尺寸的标准主要有两个:神经元个数和参数个数。以上图两个网络举例:
左侧网络有 $4+2=6$ 个神经元(输入层不算),$[3 \times 4] + [4 \times 2]=20$ 个 权重(weights),$4+2=6$ 个偏置(bias),共 $26$ 个可学习的参数。
右侧网络有 $4+4+2=10$ 个神经元(输入层不算),$[3 \times 4]+[4 \times 4]+[4 \times 1]=32$ 个权重(weights), $4+4+1=9$ 个偏置(bias),共 $41$ 个可学习的参数。
常识:现代卷积神经网络能包含约1亿个参数,可由 $10-20$ 层构成(深度学习,deep learning)。然而,有效连接(effective connections)的个数因为参数共享的缘故大大增多,这在后面CNN的章节会详细介绍。
前向传播计算举例(feed-forward computation)

不断重复的矩阵乘法和激活函数相交织。
将神经网络组织成层状的一个重要原因,就是这个结构让神经网络算法使用矩阵向量操作变得简单和高效。以上图右侧的三层神经网络举例,输入是 $[3 \times 1]$ 的向量。一个层所有连接的强度(all connections strength)可以被存在一个单独的矩阵中。如第一个隐层权重 $W_1$ 是 $[4 \times 3]$ 的,所有单元的偏置储存在 $b_1$ 中,尺寸是 $[4 \times 1]$ 。这样,每个神经元的权重保存在 $W_1$ 的一个行中(这里笔者有结合神经元结构的思考,详见下面的注释),因此矩阵乘法 np.dot(W1,x) 可以计算该层所有神经元的激活数据。类似地, $W_2$ 是 $[4 \times 4]$ 矩阵,存储第二个隐层的连接强度,$W_3$ 是 $[1 \times 4]$ 用于输出层。因此可以总结,完成的 $3$ 层神经网络的前向传播就是简单的 $3$ 次矩阵乘法,交织着激活函数的应用。
对于上图右侧的神经网络的第一个隐层(hidden layer 1),该层的每个神经元 $unit{2,i}, i \in {1,2,3,4}$ ($unit{2,i}$ 表示第 $2$ 层第 $i$ 个神经元)会接收来自上层的(这里是input layer)每个神经元传递的信号(如 $unit{1,j}, j \in {1,2,3}$ ),以进行 $unit{2,i}$ 的信号计算($\sum{j}w_jx_j, j \in {1,2,3}$,其中 $w_j$ 是 $unit{2, i}$ 对上一层第 $j$ 个神经元的权重,$x_j$ 是上一层第 $j$ 个神经元传播出的信号)。因此,将 $w_j, j \in {1,2,3}$ 写成一个 $[3 \times 1]$ 的向量即为上文中描述的“ $W_1$ 中的一个行”。
因此, $W_1$ 的尺寸为 $[4 \times 3]$ 中,$4$ 指本层的神经元个数,$3$ 指上层的神经元个数。因此容易知道 $W_2$ 的尺寸是 $[4 \times 4]$
1 | # 一个3层神经网络的前向传播: |
在上述代码中 $W_1, W_2, W_3, b_1, b_2, b_3$ 都是网络中可学习的参数。值得注意的是,$x$ 并不是一个单独的列向量,而可以是一个批量训练数据(其中每个输入样本会是 $x$ 中的一列),所有样本会被并行化地高效计算出来。
全连接层的前向(正向)传播一般就是先进行一个矩阵乘法,然后加上偏置并使用激活函数。
表达能力
理解全连接层神经网络的一个方式是,可以认为其定义了一个由一系列函数组成的函数族(family of functions),网络的权重是每个函数的参数。因此问题是:该函数族的表达能力如何?存在不能被神经网络表达的函数吗?
可以证明拥有至少一个隐层的神经网络是一个通用的近似器。对给定的任意连续函数 $f(x)$ 和任意 $\epsilon > 0$,均存在至少含一个隐层的神经网络 $g(x)$ (且网络中有合理选择的非线性激活函数,如 sigmoid ),对于 $ \forall x$ ,使得 $|f(x) - g(x)|<\epsilon$ 。换句话说,该神经网络可以近似任何连续函数。
既然一个隐层就能近似任何函数,那为什么还要构建更多层来将网络做得更深?答案是:虽然一个2层网络在数学理论上能完美地近似所有连续函数,但在实际操作中效果相对较差。在一个维度上,虽然以 $a,b,c$ 为参数向量“指示块之和”函数 $g(x)=\sum_{i}c_i \mathbb{l} (a_i < x < b_i)$ 也是通用的近似器,但是谁也不会建议在机器学习中使用这个函数公式。神经网络在实践中非常好用,是因为它们表达出的函数不仅平滑,而且对于数据的统计特性有很好的拟合。同时,网络通过最优化算法(例如梯度下降)能比较容易地学习到这个函数。类似的,虽然在理论上深层网络(使用了多个隐层)和单层网络的表达能力是一样的,但是就实践经验而言,深度网络效果比单层网络好。
另外,在实践中3层的神经网络会比2层的表现好,然而继续加深(做到4,5,6层)很少有太大帮助。卷积神经网络的情况却不同,在卷积神经网络中,对于一个良好的识别系统来说,深度是一个极端重要的因素(比如数十(以10为量级)个可学习的层)。对于该现象的一种解释观点是:因为图像拥有层次化结构(比如脸是由眼睛等组成,眼睛又是由边缘组成),所以多层处理对于这种数据就有直观意义。
层的数量和尺寸
在面对一个具体问题的时候该确定网络结构呢?到底是不用隐层呢?还是一个隐层?两个隐层或更多?每个层的尺寸该多大?
This is copyright.